
LC circuits are simple made of inductors (symbolized by L) and capacitors (sybolized by C). Let's brush up the physics behind those components. You can skip this part if you want, and jump straight to where we take a look at and calculate the electronic stuff.
A capacitor is a device used to store electrical charge. In it's simplest form, its two conductors (in most cases they are metal plates) and an isolator in between. As you apply a voltage between those, free electrons from one plate will travel to the other, forced by the electromotive force (emf) of the battery/power supply. Or rather, for each electron leaving one plate, a new one will flow onto the other plate.
Let's recall some formulas:
Electrical current is the rate of flow of electrons, so its equal to the change of charge over time:
$$ I = \frac{\Delta Q}{\Delta t} $$
(To recall: Delta ($ \Delta $) means "change of")
Capacitance is defined as the ratio of charge to voltage:
$$ C = \frac{Q}{V} $$
Lets transform the formula to get the charge: $ Q = V \cdot C $
When we charge the capacitor, the charge changes and so does the voltage. The capacitance doesnt often change
$$ \Delta Q = \Delta V \cdot C $$
And now, let's substitute that $ \Delta Q $ into our current equation:
$$ I = C \frac{\Delta V}{\Delta t} $$
The capacitor blocks DC, because at DC, $\Delta V = 0$ so $I = 0$.
The current through the capacitor is proportional to the capacitance and voltage change over time
An inductor is nothing more than some isolated wire wound into a spring, optionally around a ferromagnetic
core. When electrical current passes through it, it generates magnetic field around it.
So what happens when the current disappears, or changes its value?
The inductor will self-induce emf on its terminals. Lenz's law defines that the emf will oppose the current flow.
This means that the inductor will "fight against" the change, by creating opposite direction EMF.
Inductors are described by many factors, for us electronic engineers, the most important one is the inductance
$ L $. From Faraday's law:
$$ \Phi_b = LI $$
The EMF induced is equal to:
$$ \mathcal{E} = -\frac{\Delta \Phi_B}{\Delta t} $$
The minus is there to mark that the EMF will work agains the current flow.
Similar to capacitor, the current is likely to change. That leads to change in the magnetic flux. Inductance usually
stays the same. Therefore:
$$ \Delta \Phi_b = L \Delta I $$
Let's substitute $ \Delta \Phi_B $. We get:
$$ \mathcal{E} = -L \frac{\Delta I}{\Delta t} $$
The inductor blocks AC, because at AC the EMF will oppose the current flow stronger and stronger as $\Delta I$ gets bigger
Because we are looking at ideal inductors and capacitors, we can say that $\mathcal{E} = V$
as the equivalent series resistance, ESR,
internal parasitic resistance of the components is zero.
As a reminder, voltage source with an internal resistance of $ r $ and EMF of $\mathcal{E}$
has the following voltage on its terminals:
$$ V = \mathcal{E} - Ir $$
That is, its EMF minus the voltage drop on the resistance due to current flow.
We differ those three names a reason.
Unlike a resistor, where the voltage is proportional to the current flowing through it and it's resistance, current flowing though a capacitor depends on the change of voltage across it, and the voltage across an inductor depends on the change of current flowing through it.
That's why we use different terms to talk about their behavior.
Resistance describes resistors. Reactance describes the opposition of change in current or voltage.
Impedance is a sum of those two. Its a complex number, so complex addition is used.
In the examples below we will ingnore that to simplify them
The formulas for impedance of L and C are below. For ideal components its equal in value to the imaginary reactance
$$ Z_L = \omega L \quad Z_C = \frac{1}{\omega C} $$The new symbol, lower case omega - $ \omega $ - is angular frequency. $ \omega = 2 \pi f $
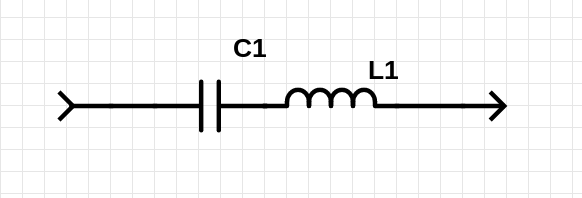
In this circuit the inductor is in series with the capacitor
Impedances in series (and paralell) are calculated the same way as resistances, so
$$ Z = Z_C + Z_L = \frac{1}{\omega C} + \omega L $$
Let's analyze what happens when we apply DC voltage to it. The inductor will oppose a change in voltage
on its terminals, and the capacitor will not pass DC current.
After the state of the circuit stabilizes, no current will flow. Let's calculate the impedance:
$$ f = 0 \quad \rightarrow \quad \omega = 2 \pi f = 0 $$
We cannot directly substitute $\omega = 0 $ because we would get division by zero, but we can calucate
the impedance as $\omega$ approaches 0
$$ Z_L = 0 \quad \quad Z_C = +\infty \quad \rightarrow \quad Z = +\infty $$
This is right - no current will flow because the impedance is infinite.
What happens as the frequency rises, approaches infinity?
$$ Z_L = +\infty \quad \quad Z_C = 0 \quad \rightarrow \quad Z = +\infty $$
There must be a point where this circuit is conducting though.
Let's express the impedance as a function of frequency:
$$ Z(\omega) = \frac{1}{\omega C} + \omega L $$
And calculate it's derivative so we can find the minimum of it, since its maxima are at zero and infinity.
$$ Z'(\omega) = -\frac{1}{\omega^2 C} + L \\
Z'(\omega) = 0 \\
-\frac{1}{\omega^2 C} + L = 0 \\
L = \frac{1}{\omega^2 C} \\
\omega^2 = \frac{1}{LC} \\
\omega = \frac{1}{\sqrt{LC}} $$
The $ \omega = \frac{1}{\sqrt{LC}} $ is the frequency at which this circuit will have the least impedance,
an ideal one will have zero impedance. Its more comonnly expressed as frequency instead of angular frequency:
$$ f = \frac{1}{2 \pi \sqrt{LC}} $$
At every other frequency the impedance will rise as the frequency is farther away.
This may be used as a band-pass filter (right) or a band-stop filter (left)
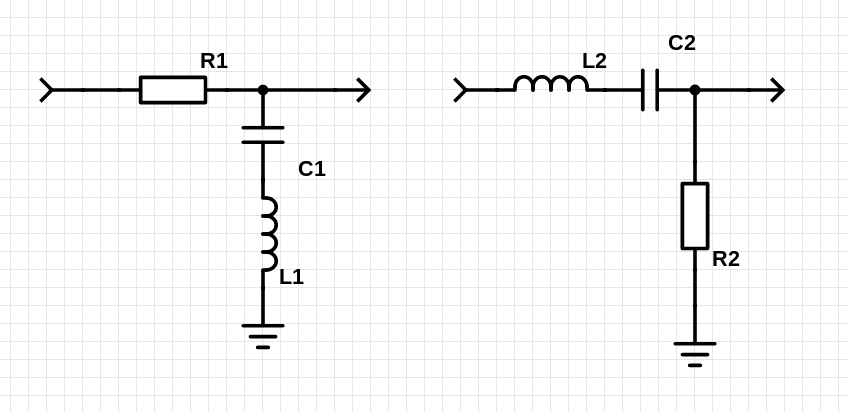
Notice that those are two "resistor dividers" if we look at the series LC filter as a resistor that's impedance is lowest at a certain frequency.
We can also connect L and C in paralell

In this case the impedance of it at DC will be zero (as the inductor will appear as a short circuit).
As the frequency of the input signal rises (approaches infinity), the capacitor will appear as a short circuit
as well so the impedance is zero, too.
The impedance of the circuit at frequency $\omega$ is:
$$ Z(\omega) = \frac{Z_L \cdot Z_C}{Z_L + Z_C} =
\frac{\omega L \cdot \frac{1}{\omega C}}{\omega L + \frac{1}{\omega C}} =
\frac{\frac{L}{C}}{\omega L + \frac{1}{\omega C}}
$$
And its derivative, pretty scary at first, is:
$$ Z'(\omega) = \frac{0 - \frac{L}{C}(L - \frac{1}{\omega^2 C})}{(\frac{1}{\omega C} + \omega L)^2} $$
But we are checking when it's zero, so after $ Z'(\omega) = 0 $ we get:
$$ 0 = - \frac{L}{C}(L - \frac{1}{\omega^2 C}) \\
0 = - \frac{L^2}{C} + \frac{L}{\omega^2 C^2} \\
\frac{L^2}{C} = \frac{L}{\omega^2 C^2} $$
simplify L and C,
$$ \frac{1}{\omega^2 C} = L \\
\frac{1}{\omega^2} = LC \\
\omega^2 = \frac{1}{LC} \\
\omega = \frac{1}{\sqrt{LC}} $$
This is the frequency at which the impedance will be maximum, as its zero both at $\omega = 0$ and
$ \omega \to \infty $.
We can use this circuit in both types of filters as well
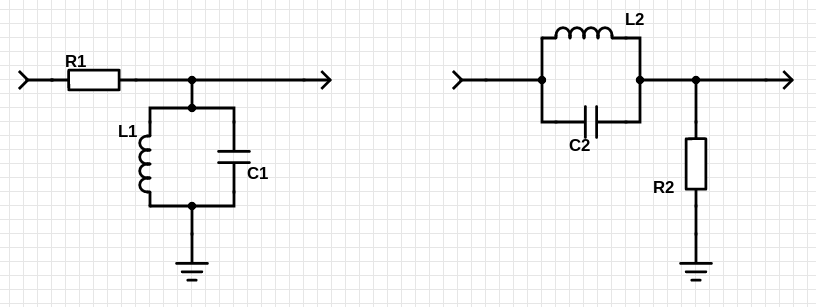
Band-pass on the left, band-stop on the right. Look at this as if it was a resistor divider, one of the resistors being the paralell LC circuit